Part I – Pose Estimation
To be written…
Part II – Reconstructing FRF Velocity from Oblique Laser Measurements
This experiment demonstrates how multiple oblique laser vibrometer measurements can be used to reconstruct the longitudinal (orthogonal) component of velocity in a vibration test.
Objective
- Reconstruct the FRF velocity vector along the Z-axis from off-axis laser measurements
- Compare different angle pairings and their reconstruction accuracy
- Use cosine projection to correct angled measurements
Methodology
Projection Correction
The laser measures the projection of the vibration along its axis. To estimate the true Z-component, each measurement was corrected using:
\[V_z = \frac{V_{\text{meas}}}{\cos(\theta)}\]This correction was applied individually to:
\[\begin{align*} \theta_{\text{M3}} &= +44.53^\circ \\ \theta_{\text{M4}} &= +22.61^\circ \\ \theta_{\text{M5}} &= -27.69^\circ \\ \theta_{\text{M6}} &= -46.09^\circ \end{align*}\]Averaging Strategy
The final reconstruction used a four-angle average:
\[Z = \frac{M3_{\text{corr}} + M4_{\text{corr}} + M5_{\text{corr}} + M6_{\text{corr}}}{4}\]Results
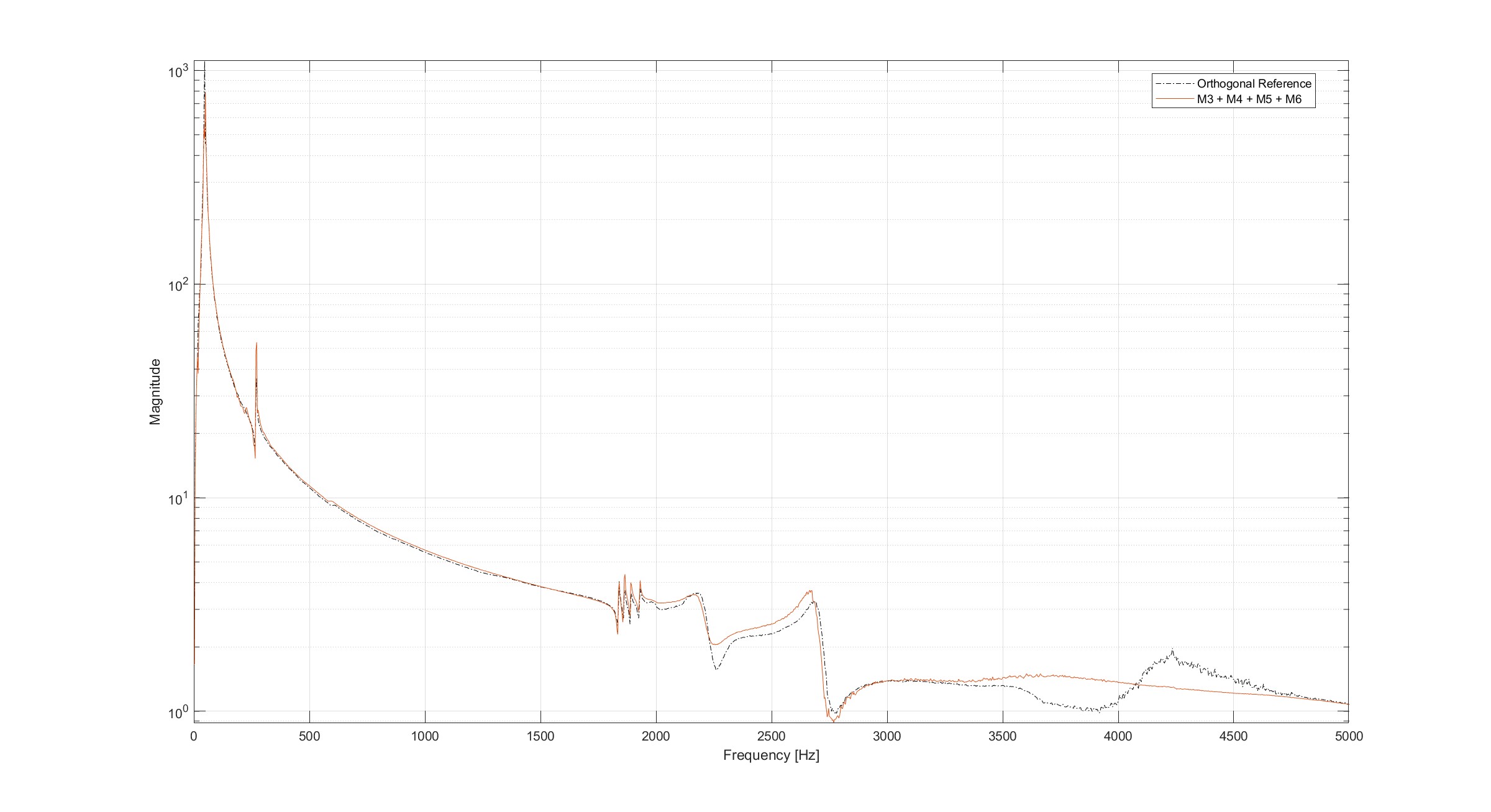
Reconstructed vs. Reference
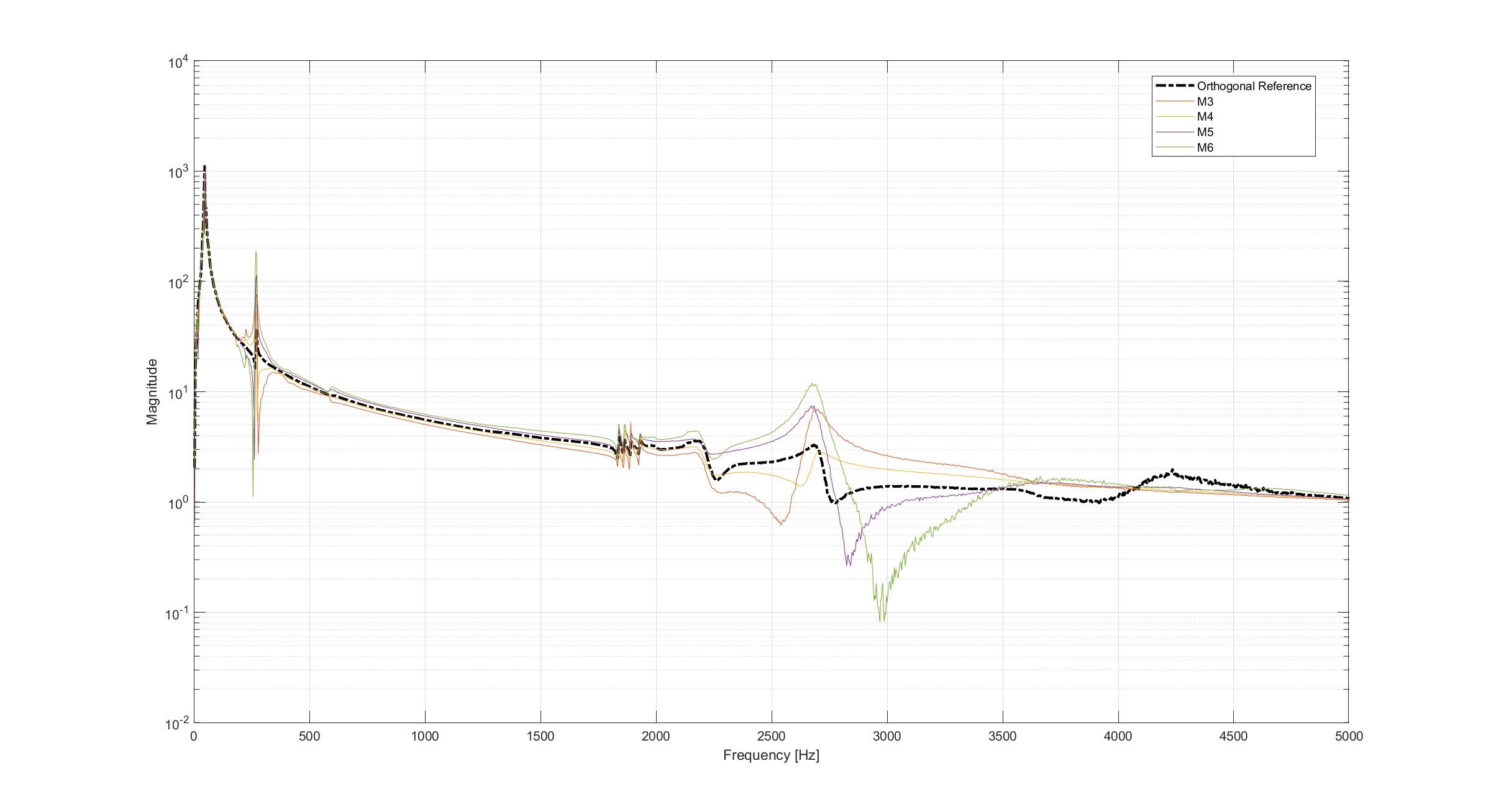
Individual Angle Contributions
This plot shows the magnitude of each corrected measurement compared to the orthogonal reference:
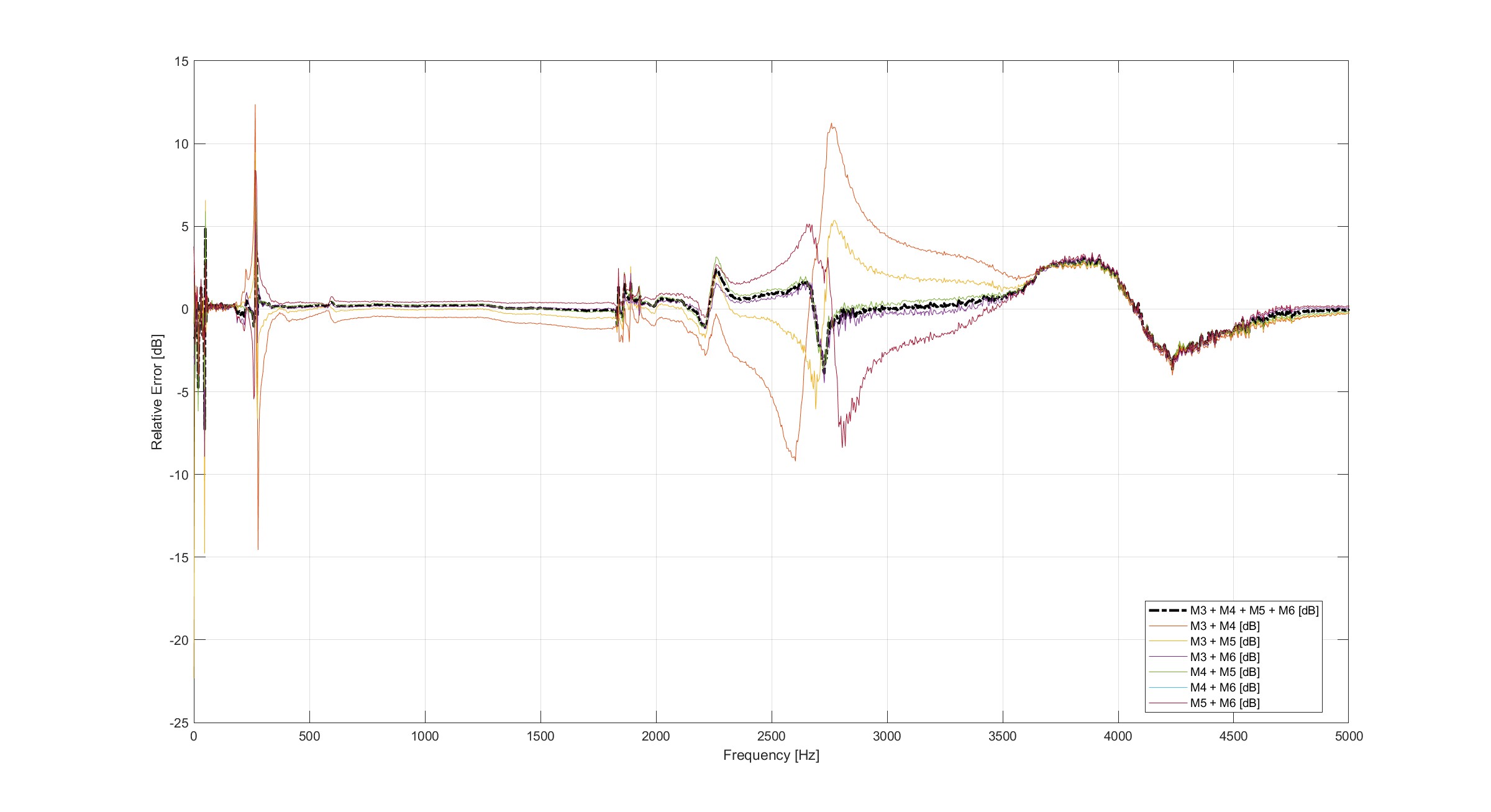
Relative Error Analysis
Relative error was computed for all pairwise reconstructions:
\[\mathrm{Error}_{\mathrm{dB}} = 20 \log_{10} \left| \frac{ \hat{V}(f) }{ V_{\text{ref}}(f) } \right|\]The best result came from the four-angle average, showing reduced error across the spectrum.
Conclusions
The main conclusions are the following:
- Projection correction using known incidence angles works effectively.
- Even strongly oblique measurements (such as 46.09°) can contribute valuable information when corrected.
- Averaging multiple corrected angles leads to a better reconstruction of the longitudinal FRF component.
Code and Data
The full source code and experimental data used are available on GitHub PhD repository.